Disciplined Convex Programming¶
Disciplined convex programming (DCP) is a system for constructing mathematical expressions with known curvature from a given library of base functions. CVXPY uses DCP to ensure that the specified optimization problems are convex.
This section of the tutorial explains the rules of DCP and how they are applied by CVXPY.
Visit dcp.stanford.edu for a more interactive introduction to DCP.
Expressions¶
Expressions in CVXPY are formed from variables, parameters, numerical
constants such as Python floats and Numpy matrices, the standard
arithmetic operators +, -, *, /, @, and a library of
functions. Here are some examples of CVXPY expressions:
import cvxpy as cp
# Create variables and parameters.
x, y = cp.Variable(), cp.Variable()
a, b = cp.Parameter(), cp.Parameter()
# Examples of CVXPY expressions.
3.69 + b/3
x - 4*a
sqrt(x) - minimum(y, x - a)
maximum(2.66 - sqrt(y), square(x + 2*y))
Expressions can be scalars, vectors, or matrices. The dimensions of an expression are stored as expr.shape.
The total number of entries is given by expr.size,
while the number of dimensions is given by expr.ndim.
CVXPY will raise an exception if an
expression is used in a way that doesn’t make sense given its
dimensions, for example adding matrices of different size.
The semantics for how shapes behave under arithmetic operations
are the same as for NumPy ndarrays (except some broadcasting is banned).
import numpy
X = cp.Variable((5, 4))
A = numpy.ones((3, 5))
# Use expr.shape to get the dimensions.
print("dimensions of X:", X.shape)
print("size of X:", X.size)
print("number of dimensions:", X.ndim)
print("dimensions of sum(X):", cp.sum(X).shape)
print("dimensions of A @ X:", (A @ X).shape)
# ValueError raised for invalid dimensions.
try:
A + X
except ValueError, e:
print(e)
dimensions of X: (5, 4)
size of X: 20
number of dimensions: 2
dimensions of sum(X): ()
dimensions of A @ X: (3, 4)
Cannot broadcast dimensions (3, 5) (5, 4)
CVXPY uses DCP analysis to determine the sign and curvature of each expression.
Sign¶
Each (sub)expression is flagged as positive (non-negative), negative (non-positive), zero, or unknown.
The signs of larger expressions are determined from the signs of their subexpressions. For example, the sign of the expression expr1*expr2 is
Zero if either expression has sign zero.
Positive if expr1 and expr2 have the same (known) sign.
Negative if expr1 and expr2 have opposite (known) signs.
Unknown if either expression has unknown sign.
The sign given to an expression is always correct. But DCP sign analysis
may flag an expression as unknown sign when the sign could be figured
out through more complex analysis. For instance, x*x is positive but
has unknown sign by the rules above.
CVXPY determines the sign of constants by looking at their value. For scalar constants, this is straightforward. Vector and matrix constants with all positive (negative) entries are marked as positive (negative). Vector and matrix constants with both positive and negative entries are marked as unknown sign.
The sign of an expression is stored as expr.sign:
x = cp.Variable()
a = cp.Parameter(nonpos=True)
c = numpy.array([1, -1])
print("sign of x:", x.sign)
print("sign of a:", a.sign)
print("sign of square(x):", cp.square(x).sign)
print("sign of c*a:", (c*a).sign)
sign of x: UNKNOWN
sign of a: NONPOSITIVE
sign of square(x): NONNEGATIVE
sign of c*a: UNKNOWN
Curvature¶
Each (sub)expression is flagged as one of the following curvatures (with respect to its variables)
Curvature |
Meaning |
|---|---|
constant |
\(f(x)\) independent of \(x\) |
affine |
\(f(\theta x + (1-\theta)y) = \theta f(x) + (1-\theta)f(y), \; \forall x, \; y,\; \theta \in [0,1]\) |
convex |
\(f(\theta x + (1-\theta)y) \leq \theta f(x) + (1-\theta)f(y), \; \forall x, \; y,\; \theta \in [0,1]\) |
concave |
\(f(\theta x + (1-\theta)y) \geq \theta f(x) + (1-\theta)f(y), \; \forall x, \; y,\; \theta \in [0,1]\) |
unknown |
DCP analysis cannot determine the curvature |
using the curvature rules given below. As with sign analysis, the conclusion is always correct, but the simple analysis can flag expressions as unknown even when they are convex or concave. Note that any constant expression is also affine, and any affine expression is convex and concave.
Curvature rules¶
DCP analysis is based on applying a general composition theorem from convex analysis to each (sub)expression.
\(f(\text{expr}_1, \text{expr}_2, ..., \text{expr}_n)\) is convex if \(\text{ } f\) is a convex function and for each \(\text{expr}_{i}\) one of the following conditions holds:
\(f\) is increasing in argument \(i\) and \(\text{expr}_{i}\) is convex.
\(f\) is decreasing in argument \(i\) and \(\text{expr}_{i}\) is concave.
\(\text{expr}_{i}\) is affine or constant.
\(f(\text{expr}_1, \text{expr}_2, ..., \text{expr}_n)\) is concave if \(\text{ } f\) is a concave function and for each \(\text{expr}_{i}\) one of the following conditions holds:
\(f\) is increasing in argument \(i\) and \(\text{expr}_{i}\) is concave.
\(f\) is decreasing in argument \(i\) and \(\text{expr}_{i}\) is convex.
\(\text{expr}_{i}\) is affine or constant.
\(f(\text{expr}_1, \text{expr}_2, ..., \text{expr}_n)\) is affine if \(\text{ } f\) is an affine function and each \(\text{expr}_{i}\) is affine.
If none of the three rules apply, the expression \(f(\text{expr}_1, \text{expr}_2, ..., \text{expr}_n)\) is marked as having unknown curvature.
Whether a function is increasing or decreasing in an argument may depend
on the sign of the argument. For instance, square is increasing for
positive arguments and decreasing for negative arguments.
The curvature of an expression is stored as expr.curvature:
x = cp.Variable()
a = cp.Parameter(nonneg=True)
print("curvature of x:", x.curvature)
print("curvature of a:", a.curvature)
print("curvature of square(x):", cp.square(x).curvature)
print("curvature of sqrt(x):", cp.sqrt(x).curvature)
curvature of x: AFFINE
curvature of a: CONSTANT
curvature of square(x): CONVEX
curvature of sqrt(x): CONCAVE
Infix operators¶
The infix operators +, -, *, / and matrix multiplication @
are treated exactly like functions.
The infix operators + and - are affine, so the rules above are
used to flag the curvature. For example, expr1 + expr2 is flagged as
convex if expr1 and expr2 are convex.
expr1*expr2, expr1/expr2, and expr1@expr2
can only be DCP when one of the expressions is constant.
The curvature rules above apply. For example, expr1/expr2 is convex when
expr1 is concave and expr2 is negative and constant.
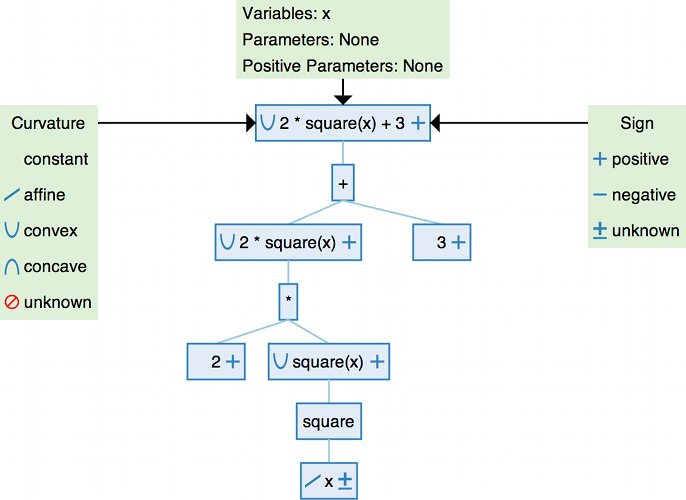
Example 1¶
DCP analysis breaks expressions down into subexpressions. The tree
visualization below shows how this works for the expression
2*square(x) + 3. Each subexpression is shown in a blue box. We mark
its curvature on the left and its sign on the right.
Example 2¶
We’ll walk through the application of the DCP rules to the expression
sqrt(1 + square(x)).
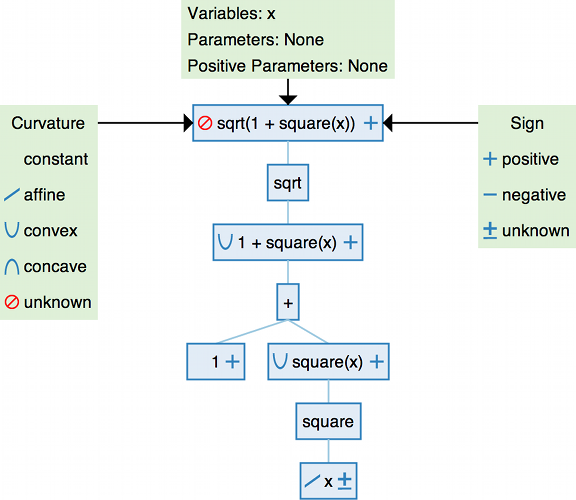
The variable x has affine curvature and unknown sign. The square
function is convex and non-monotone for arguments of unknown sign. It
can take the affine expression x as an argument; the result
square(x) is convex.
The arithmetic operator + is affine and increasing, so the
composition 1 + square(x) is convex by the curvature rule for convex
functions. The function sqrt is concave and increasing, which means
it can only take a concave argument. Since 1 + square(x) is convex,
sqrt(1 + square(x)) violates the DCP rules and cannot be verified as
convex.
In fact, sqrt(1 + square(x)) is a convex function of x, but the
DCP rules are not able to verify convexity. If the expression is written
as norm(hstack(1, x), 2), the L2 norm of the vector \([1,x]\),
which has the same value as sqrt(1 + square(x)), then it will be
certified as convex using the DCP rules.
print("sqrt(1 + square(x)) curvature:",
cp.sqrt(1 + cp.square(x)).curvature)
print("norm(hstack([1, x]), 2) curvature:",
cp.norm(cp.hstack([1, x]), 2).curvature)
sqrt(1 + square(x)) curvature: UNKNOWN
norm(hstack(1, x), 2) curvature: CONVEX
DCP problems¶
A problem is constructed from an objective and a list of constraints. If a problem follows the DCP rules, it is guaranteed to be convex and solvable by CVXPY. The DCP rules require that the problem objective have one of two forms:
Minimize(convex)
Maximize(concave)
The only valid constraints under the DCP rules are
affine == affine
convex <= concave
concave >= convex
You can check that a problem, constraint, or objective satisfies the DCP
rules by calling object.is_dcp(). Here are some examples of DCP and
non-DCP problems:
x = cp.Variable()
y = cp.Variable()
# DCP problems.
prob1 = cp.Problem(cp.Minimize(cp.square(x - y)),
[x + y >= 0])
prob2 = cp.Problem(cp.Maximize(cp.sqrt(x - y)),
[2*x - 3 == y,
cp.square(x) <= 2])
print("prob1 is DCP:", prob1.is_dcp())
print("prob2 is DCP:", prob2.is_dcp())
# Non-DCP problems.
# A non-DCP objective.
obj = cp.Maximize(cp.square(x))
prob3 = cp.Problem(obj)
print("prob3 is DCP:", prob3.is_dcp())
print("Maximize(square(x)) is DCP:", obj.is_dcp())
# A non-DCP constraint.
prob4 = cp.Problem(cp.Minimize(cp.square(x)),
[cp.sqrt(x) <= 2])
print(f"prob4 is DCP: {prob4.is_dcp()}")
print(f"sqrt(x) <= 2 is DCP: {(cp.sqrt(x) <= 2).is_dcp()}")
prob1 is DCP: True
prob2 is DCP: True
prob3 is DCP: False
Maximize(square(x)) is DCP: False
prob4 is DCP: False
sqrt(x) <= 2 is DCP: False
CVXPY will raise an exception if you call problem.solve() on a
non-DCP problem.
# A non-DCP problem.
prob = cp.Problem(cp.Minimize(cp.sqrt(x)))
try:
prob.solve()
except Exception as e:
print(e)
Problem does not follow DCP rules.