Fractional optimization

This notebook shows how to solve a simple concave fractional problem, in which the objective is to maximize the ratio of a nonnegative concave function and a positive convex function. Concave fractional problems are quasiconvex programs (QCPs). They can be specified using disciplined quasiconvex programming (DQCP), and hence can be solved using CVXPY.

!pip install --upgrade cvxpy

import cvxpy as cp
import numpy as np
import matplotlib.pyplot as plt

Our goal is to maximize the function

\[\frac{\sqrt{x}}{\exp(x)}.\]

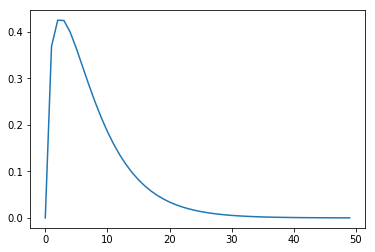
This function is not concave, but it is quasiconcave, as can be seen by inspecting its graph.

plt.plot([np.sqrt(y) / np.exp(y) for y in np.linspace(0, 10)])
plt.show()

The below code specifies and solves the QCP, using DQCP. The concave fraction function is DQCP-compliant, because the ratio atom is quasiconcave (actually, quasilinear), increasing in the numerator when the denominator is positive, and decreasing in the denominator when the numerator is nonnegative.

x = cp.Variable()
concave_fractional_fn = cp.sqrt(x) / cp.exp(x)
problem = cp.Problem(cp.Maximize(concave_fractional_fn))
assert problem.is_dqcp()
problem.solve(qcp=True)

0.4288821220397949

x.value

array(0.50000165)