Nonnegative matrix factorization

A derivative work by Judson Wilson, 6/2/2014.

Adapted from the CVX example of the same name, by Argyris Zymnis,

Joelle Skaf and Stephen Boyd

Introduction

We are given a matrix \(A \in \mathbf{\mbox{R}}^{m \times n}\) and are interested in solving the problem:

\[\begin{split}\begin{array}{ll} \mbox{minimize} & \| A - YX \|_F \\ \mbox{subject to} & Y \succeq 0 \\ & X \succeq 0, \end{array}\end{split}\]

where \(Y \in \mathbf{\mbox{R}}^{m \times k}\) and \(X \in \mathbf{\mbox{R}}^{k \times n}\).

This example generates a random matrix \(A\) and obtains an approximate solution to the above problem by first generating a random initial guess for \(Y\) and then alternatively minimizing over \(X\) and \(Y\) for a fixed number of iterations.

Generate problem data

import cvxpy as cp
import numpy as np

# Ensure repeatably random problem data.
np.random.seed(0)

# Generate random data matrix A.
m = 10
n = 10
k = 5
A = np.random.rand(m, k).dot(np.random.rand(k, n))

# Initialize Y randomly.
Y_init = np.random.rand(m, k)

Perform alternating minimization

# Ensure same initial random Y, rather than generate new one
# when executing this cell.
Y = Y_init

# Perform alternating minimization.
MAX_ITERS = 30
residual = np.zeros(MAX_ITERS)
for iter_num in range(1, 1+MAX_ITERS):
    # At the beginning of an iteration, X and Y are NumPy
    # array types, NOT CVXPY variables.

    # For odd iterations, treat Y constant, optimize over X.
    if iter_num % 2 == 1:
        X = cp.Variable(shape=(k, n))
        constraint = [X >= 0]
    # For even iterations, treat X constant, optimize over Y.
    else:
        Y = cp.Variable(shape=(m, k))
        constraint = [Y >= 0]

    # Solve the problem.
    # increase max iters otherwise, a few iterations are "OPTIMAL_INACCURATE"
    # (eg a few of the entries in X or Y are negative beyond standard tolerances)
    obj = cp.Minimize(cp.norm(A - Y*X, 'fro'))
    prob = cp.Problem(obj, constraint)
    prob.solve(solver=cp.SCS, max_iters=10000)

    if prob.status != cp.OPTIMAL:
        raise Exception("Solver did not converge!")

    print('Iteration {}, residual norm {}'.format(iter_num, prob.value))
    residual[iter_num-1] = prob.value

    # Convert variable to NumPy array constant for next iteration.
    if iter_num % 2 == 1:
        X = X.value
    else:
        Y = Y.value

Iteration 1, residual norm 2.766300564135502
Iteration 2, residual norm 0.5840356930600721
Iteration 3, residual norm 0.3356679970549085
Iteration 4, residual norm 0.18670276027770083
Iteration 5, residual norm 0.12819921698143966
Iteration 6, residual norm 0.09295501592922492
Iteration 7, residual norm 0.06766021043574907
Iteration 8, residual norm 0.04958204907945361
Iteration 9, residual norm 0.03897402158866238
Iteration 10, residual norm 0.02979328283505179
Iteration 11, residual norm 0.022938564327729952
Iteration 12, residual norm 0.021943924920767337
Iteration 13, residual norm 0.01810297853945281
Iteration 14, residual norm 0.014551161988556204
Iteration 15, residual norm 0.014039687334395924
Iteration 16, residual norm 0.009354606824469416
Iteration 17, residual norm 0.008643141637584189
Iteration 18, residual norm 0.007278100007476402
Iteration 19, residual norm 0.008486679700021057
Iteration 20, residual norm 0.008827511916396866
Iteration 21, residual norm 0.008396764193205366
Iteration 22, residual norm 0.005265185332845983
Iteration 23, residual norm 0.006931929503816392
Iteration 24, residual norm 0.007356156596477946
Iteration 25, residual norm 0.0039053948996930054
Iteration 26, residual norm 0.003989885269615319
Iteration 27, residual norm 0.002920361405226024
Iteration 28, residual norm 0.007779246694466739
Iteration 29, residual norm 0.007339011292898449
Iteration 30, residual norm 0.005008539285258121

Output results

#
# Plot residuals.
#

import matplotlib.pyplot as plt

# Show plot inline in ipython.
%matplotlib inline

# Set plot properties.
plt.rc('text', usetex=True)
plt.rc('font', family='serif')
font = {'weight' : 'normal',
        'size'   : 16}
plt.rc('font', **font)

# Create the plot.
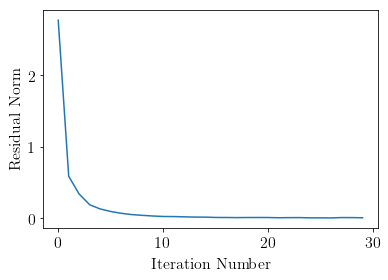
plt.plot(residual)
plt.xlabel('Iteration Number')
plt.ylabel('Residual Norm')
plt.show()

#
# Print results.
#
print('Original matrix:')
print(A)
print('Left factor Y:')
print(Y)
print('Right factor X:')
print(X)
print('Residual A - Y * X:')
print(A - Y.dot(X))
print('Residual after {} iterations: {}'.format(iter_num, prob.value))

Original matrix:
[[1.323426   1.11061189 1.69137835 1.20020115 1.13216889 0.5980743
  1.64965406 0.340611   1.69871738 0.78278448]
 [1.73721109 1.40464204 1.90898877 1.60774132 1.53717253 0.62647405
  1.76242265 0.41151492 1.8048194  1.20313124]
 [1.4071438  1.10269406 1.75323063 1.18928983 1.23428169 0.60364688
  1.63792853 0.40855006 1.57257432 1.17227344]
 [1.3905141  1.33367163 1.07723947 1.67735654 1.33039096 0.42003169
  1.22641711 0.21470465 1.47350799 0.84931787]
 [1.42153652 1.13598552 2.00816457 1.11463462 1.17914429 0.69942578
  1.90353699 0.45664487 1.81023916 1.09668578]
 [1.60813803 1.23214532 1.73741086 1.3148874  1.27589039 0.40755835
  1.31904948 0.3469129  1.34256526 0.76924618]
 [0.90607895 0.6632877  1.25412229 0.81696721 0.87218892 0.50032884
  1.245879   0.25079329 1.25017792 0.72155621]
 [1.5691922  1.47359672 1.76518996 1.66268312 1.43746574 0.72486628
  1.97409333 0.39239642 2.09234807 1.16325748]
 [1.18723548 1.00282008 1.41532595 1.03836298 0.90382914 0.38460446
  1.213473   0.23641422 1.32784402 0.27179726]
 [0.75789915 0.75119989 0.99502166 0.65444815 0.56073096 0.341146
  1.02555143 0.24273668 1.01035919 0.49427978]]
Left factor Y:
[[ 7.56475742e-01  3.42102372e-01  8.40426641e-01  7.02845111e-01
   4.38002833e-03]
 [ 6.36189366e-01  8.27831861e-01  5.28165827e-01  5.60609403e-01
   3.34595403e-02]
 [ 5.54834858e-01  6.37954560e-01  8.01726231e-01  1.96879041e-01
   3.74736667e-02]
 [ 2.72955779e-01  9.53749151e-01  6.14934798e-02  9.81276972e-01
  -4.26647247e-05]
 [ 7.93952558e-01  3.50946872e-01  1.18853643e+00  3.85961318e-01
   2.96701863e-02]
 [ 7.26183347e-01  4.41639937e-01  2.71711699e-03  7.33393633e-01
   4.55176129e-02]
 [ 4.89263105e-01  4.20725095e-01  7.56036398e-01  6.24033457e-02
  -5.38302416e-04]
 [ 6.09810836e-01  7.55780427e-01  1.03636918e+00  9.08549910e-01
   1.91844947e-03]
 [ 8.31578328e-01  8.75528332e-05  2.93543168e-01  1.10037225e+00
  -2.65884776e-04]
 [ 4.26650967e-01  5.53761974e-02  6.52855369e-01  6.43132832e-01
   1.47569255e-02]]
Right factor X:
[[ 1.07015116e+00  4.25961964e-01  1.59511553e+00  6.26808607e-01
   8.98124301e-01  3.62801718e-01  9.53757673e-01  1.88661317e-01
   9.64559055e-01  1.43675625e-01]
 [ 8.72908811e-01  7.03553498e-01  6.45229205e-01  1.10121868e+00
   9.93621271e-01  3.12383803e-01  7.45085312e-01  1.25155585e-01
   8.84272390e-01  7.94988511e-01]
 [ 1.41086863e-04  1.70049131e-01  2.73427259e-01  2.50933223e-02
   8.38007474e-03  2.51575697e-01  5.99473425e-01  1.39362252e-01
   5.06840502e-01  4.22844259e-01]
 [ 2.70906925e-01  5.46340550e-01  1.04256418e-02  4.63290841e-01
   1.39889787e-01  7.65220031e-03  2.22742919e-01  3.60875098e-02
   3.41601146e-01  2.72448408e-02]
 [ 5.44108256e+00  4.62667224e+00  6.26354249e+00  7.23656013e-01
   1.81220987e+00 -2.57729003e-07  2.90739234e+00  2.81123997e+00
  -2.15606388e-06  6.43189790e+00]]
Residual A - Y * X:
[[ 9.02157264e-04  5.23117764e-04 -5.79950842e-04 -5.74317402e-04
  -4.61768644e-04 -5.28680186e-05  1.62394448e-04  2.76277321e-04
   4.85227596e-04 -5.60481823e-04]
 [-2.33027425e-04  3.21455250e-04  2.17040399e-04  1.56606195e-04
  -2.41256203e-04 -1.01386736e-04  7.36342995e-05 -1.73587325e-05
  -5.22429324e-05 -2.04432888e-04]
 [-8.35846517e-04  2.46121871e-04  5.93720663e-04  5.38806481e-04
  -8.42363429e-05 -1.36215640e-04  2.31633730e-06 -1.52108618e-04
  -3.23620331e-04 -5.42078084e-06]
 [ 2.62860853e-04  1.83780003e-05 -3.20542830e-04 -1.49712163e-04
  -1.31334078e-04  8.78805144e-05  1.46798183e-04 -2.03546983e-05
   4.79256197e-04 -5.81320754e-04]
 [-6.22557723e-04  6.31892711e-04  4.34719938e-04  4.01388769e-04
  -3.52745774e-04 -2.12014739e-04  8.42548761e-05 -4.17321003e-05
  -1.50760383e-04 -3.01455643e-04]
 [-8.46202248e-04  3.61714835e-04  6.15005890e-04  5.85452470e-04
  -2.39872783e-04 -1.59000367e-04  6.24749082e-05 -1.69461803e-04
  -3.16622183e-04 -8.20910778e-05]
 [ 1.15561552e-03 -1.28864368e-03 -1.77288000e-03 -5.10264071e-04
   6.38713553e-04  7.17730381e-04  2.05892579e-04 -2.69449092e-04
   1.71225020e-03 -1.13410340e-03]
 [ 1.57913703e-04  6.21168134e-04 -4.04695033e-05 -1.48187018e-04
  -4.38037868e-04 -1.45409129e-04  1.34145488e-04  1.47289692e-04
   1.98184939e-04 -5.09549810e-04]
 [ 5.51365483e-04 -1.32683206e-03 -1.26345269e-03  6.01647636e-05
   9.72529426e-04  6.10472383e-04 -1.48674297e-05 -3.54468161e-04
   9.92202367e-04 -1.42249517e-04]
 [-1.63514531e-03 -1.59800828e-04  1.08957766e-03  1.01954949e-03
   3.41048252e-04 -1.06257705e-04 -1.57094132e-04 -3.64204427e-04
  -7.26930797e-04  4.63755883e-04]]
Residual after 30 iterations: 0.005008539285258121